4. Idő és tér
A fizika tudománya valamikor a 15. században kezdődött. Ekkor éltek olyan híres emberek, mint Kopernikusz, Kepler, Galilei, Newton és társai. Kopernikusz a napközpontú világképet javasolt. Kepler módosította ebben a modellben a bolygók pályát ellipszisre. Newton rájött az általános tömegvonzás törvényeire. Galilei pedig arra, hogy a szabadon ejtett, vagy lejtőn guruló test által megtett út az idő négyzetével arányos.
Szabadon eső test által megtett út az eltelt idő négyzetével arányos. Nagyon sokat kellett várni, hogy elég pontos óránk legyen, amely alkalmas ennek az összefüggésnek a meghatározásához.
Viszont ahhoz, hogy ezeket a modelleket igazolni tudjuk, képesnek kell lennünk arra, hogy mérjük az időt és a távolságokat. Akár olyan időket és távolságokat is, amelyek emberi léptékkel már nem foghatók fel.
Az idő
Nehéz arra kérdésre válaszolni, hogy mi is az idő. De nem is a definíció a fontos, hanem az, hogy hogyan mérjük, és tartjuk számon azt.
Hogyan mértük az időt, amíg nem volt sehol egy szabványos óra, amelyhez lehetne mérni? Van egyetlen egy dolog, ami nagyjából elég szabványos. Ez pedig a Nap járása. Az egyik nap megnézzük, hogy a Nap mikor jár a legmagasabban az égen. Majd következő nap ismét feljegyezzük, a két delelés között eltelt időtartam az 1 nap. Ez az időtartam minden nap megmérhető, és sokáig ez volt az időszabvány alapja. Tehát a másodperc definíciója sokáig az átlagos nap hosszának az 1/86400-ed része volt.
A nap túl hosszú időtartam, a gyakorlatban szükségünk van jóval rövidebb idők mérésére is. Eleinte csak simán felosztották napóra számlapját órákra. Később az órákat is tovább osztották, percekre. Azonban a legjobban beállított napóra is legfeljebb perc pontossággal képes mérni. Többi óra, mint például a vízóra vagy a homokóra nem volt alkalmas rövidebb időtartamok mérésére. A 15. században jelentek meg a rúgós órák, amelyek már képesek voltak másodpercek mérésére is. Bár hosszú távon nem voltak valami pontosak. Ezekben a rúgó csak a felhúzáskor tárolta az energiát és nem a pontosságot szolgálta. Majd később a 17. században készítették el az első ingaórát. Ennek a működési elve az, hogy az inga (egy madzagra vagy rúdra erősített súly) oda-vissza lengési ideje állandó. Ha biztosítják az állandó hőmérsékletet, és nem mozgatják az órát (gravitáció), akkor nagyon pontos időmérést tesz lehetővé. Egészen a 20. század elejéig ilyen ingaóra biztosította a szabványos időt.
Majd a 20. század elején megjelentek a kvarcórák. Amelyek felváltották az ingaórát. A kvarckristálynak van egy olyan tulajdonsága, hogyha deformálják, akkor a két vége között elektromos feszültség generálódik. Illetve a dolog fordítva is igaz: hogyha feszültséget kapcsolunk rá, akkor is deformálódik. A kvarcórákban egy pici kvarckristály van, aminek az önrezgésszáma 32768 Hz (ez az a frekvencia, amin a kvarc „csilingel”, ha megütik). Ezt a frekvenciát felhasználva elektromos impulzusokkal fenntartva a rezgést ez a kristály folyamatosan rezgésben tartható. Aztán ezt a rezgést 15 felező áramkörön átvezetve eljutunk a másodpercenkénti 1 jelhez, amellyel az elektronikus LCD számlapú óra működtethető. Hogy milyen kis időintervallum mérhető egy órával az attól függ, hogy milyen sűrűn „tiktakol”. Egy ingaóra talán 2-szer egy másodpercben, míg egy kvarcóra már 32768-szor, ezért egy ilyennel kimérhető az 1 másodperc tízezredének megfelelő időtartam is.
Kristályokkal megahertzes nagyságrendű frekvencia érhető el. Ez azt jelenti, hogy egy 10 MHz-es órával 10-7 másodperc nagyságrendű idők mérhetők. De csak akkor, hogyha állandó hőmérsékleten tartják, és a mechanikus ütődésektől védik (amitől maradandóan deformálódhat a kristály). Ettől függetlenül a technológia alkalmas pontos idő mérésére karórákban a hőmérséklet érzékenység ellenére is.
A 60-as évektől kezdve ismét egy forradalom volt az időmérésben. Ekkor találták fel az atomórát. Ennek a működésének a lényege, hogy az atomok különböző energiaszinteken lehetnek csak (az energiaátmenet kvantált). Így ha egy elektron az atomban egy magasabb energiaszintről egy alacsonyabb energiaszintre ugrik le, akkor az energiakülönbségnek megfelelő fotont bocsátja ki; vagy elnyel egyet, hogyha az alacsonyabbról ugrik fentebb. Először kiválogatjuk az alacsony energiaszinten lévő atomokat. Majd sugárzásnak tesszük ki. Hogyha sikerült ráhangolódnunk a megfelelő frekvenciára, akkor ezek az alacsony szintű atomok felugorhatnak a magasabb szintre. Ezen magasabb szintű atomok számolásával eltalálható az a frekvencia, amely az átmenetre jellemző (a legtöbb felugrálás akkor van, amikor a frekvencia pont jó). Gyakorlatban a céziumot használják erre, az energiaátmenethez tartozó foton frekvenciája pedig pontosan 9 192 631 770 Hz (9,1 GHz rádióhullámú sáv). Azért pontosan ennyi, mert ennyinek definiálták. A cézium a két állapota között másodpercenként ennyiszer történik az átmenet, amikor az atom rezeg. Ha nem ennyit rezegne, akkor a másodpercet igazítanánk hozzá, hogy ennyit rezegjen. Ez a jelenlegi a szabvány, és így definiálják a másodpercet. Egy atomóra olyan pontos, hogy több millió év alatt tévedne 1 másodpercet.
Elektronikus áramkörökkel nagyjából a THz frekvencia érhető el, ez azt is jelenti, hogy ezekkel az áramkörökkel, kb. 10-11 másodperc pontossággal lehet időtartamokat mérni. Jelenleg ennél rövidebb ideig tartó eseményeket csak közvetett módon lehet mérni. Tegyük fel, hogy egy részecskegyorsítóban meghatároztuk egy részecske lendületét és sebességét a kialakulása után. Ha a részecske a fénysebesség 80%-ával mozgott tehát kb. 240000 km/s sebességgel, és megtett 0,24 mm-t mielőtt elbomlott volna, akkor ebből ki lehet következtetni, hogy 1 pikomásodpercet (azaz 10-12 s) létezett. Még rövidebb időtartamú dolgokat lehet megfigyelni femtomásodperces nagyon rövid lézerimpulzusokkal. Ezek a rövid impulzusok úgy működnek, mint egy vaku, minél rövidebb a villanás, annál kisebb a bemozdulás esélye. Így nagyon rövid ideig tartó események válnak mérhetővé.
Volt szó a rövid időtartamokról, de mi a helyzet a hosszúakkal. Nincs különösebb problémánk az évszak és évek mérésével, de még az évtizedekével sem. Például megtudhatjuk, hogy egy fát hány évesen vágták ki az évgyűrűinek a számából. Bizonyos régi történelmi események óta eltelt időket meghatározhatjuk, hogyha szétnézünk egy történelmi levéltárban. Egyes események pontos megállapításában sokat segít, hogyha az adott területen teljes napfogyatkozás volt. Ugyanis viszonylag egyszerűen kiszámolható számítógéppel, hogy régen mikor voltak a Föld egyes pontjain napfogyatkozások. Ha egy régi krónikás elsötétülő napról írt egy adott országban, akkor ebből napra pontosan meg lehet állapítani, hogy mikor történt az adott dolog.
Vannak azonban olyan régen történt dolgok, amelyekről nem íródott krónika. Például adott egy fosszília, meg kéne határozni, hogy az állat mikor pusztult el. A segítséget a kozmikus részecskék adják. A levegő legnagyobb része nitrogén. Méghozzá a 7-es rendszámú nitrogén-14 izotóp. Ha ezt eltalálja egy nagy sebességű kozmikus neutron, akkor kiüthet belőle egy protont és a helyére állhat. Így lesz belőle 1 rendszámmal kisebb, de nagyjából azonos tömegű szén-14 izotóp. Ez a szén-14 izotóp radioaktív, ez az extra neutron hajlamos visszaalakulni egy protonná benne, miközben kilök egy elektront magából. Így visszaalakul nitrogén-14 atommá. A kozmikus részecskék révén folyamatosan keletkezik a szén-14, és magától folyamatosan alakul is vissza nitrogénné. Ez a folyamat egyensúlyban van. Az élőlények, miközben esznek, az életük során folyamatosan veszik fel a szenet. Köztük ezt a radioaktív fajtát is. Persze különösen aggódni nem kell miatta, mert 1000 milliárd szénatomból csak 1 ez a radioaktív fajta. Azonban, amint egy élőlény elpusztul, többé nem vesz fel újabb szenet. A pusztulás időpontjában a testében fennáll ez az arány szén-14 és a másfajta szén között. A szén-14 atomok fele kb. 6000 év alatt bomlik el. Tehát ha ezt a fosszíliát újra megnézzük 6000 év múlva, már csak szén-14 atomoknak a fele lesz meg. Ha 12000 év múlva nézzük meg, akkor már csak a negyede, 18000 év múlva már csak a nyolcada, stb. Ez az izotóparány tömegspektrométer segítségével pontosan meghatározható, és kb. 60000 évre visszamenőleg használható. Honnét tudjuk, hogy kezdetben mekkora volt ez az izotóparány? Itt feltételezzük, hogy a kozmikus sugárzás mértéke, és a föld légkörének az összetétele nem változott komolyabb mértékben az utolsó 100000 évben. Erre a feltételre épül ez a radiokarbon kormeghatározás. Nyilván napra, percre pontos eredményt nem tudunk ezzel adni, de az évszázad nagyjából belőhető vele.
De mi a helyzet a régebbi dolgokkal? Honnét tudjuk például, hogy a Föld milyen idős? Itt is nagyon hasonló az elv, mint a szén-14 időmeghatározásnál. Létezik egy ásvány, úgy hívják, hogy cirkon (ZrSiO4). Ez egy rendkívül stabil vegyület, ellenáll az idő vasfogának, és a legtöbb természetben előforduló kémiai vegyületnek is. Ez a kristály akkor keletkezik, amikor a vulkánból feltörő magma megszilárdul. És van egy nagyon fontos tulajdonsága: a kristályrácsába nem tud beépülni az ólom, viszont be tud épülni az urán (ennek oka a két elem elektronszerkezetének a különbségében keresendő). Így a kialakuláskor a cirkonban nem lehet ólom, viszont lehet benne urán. Az urán radioaktív. Viszont nem annyira aktív, mint a szén-14, az természetben leginkább megtalálható (92-es rendszámú) urán-238 izotóp mennyisége kb. 4,5 milliárd év alatt feleződik meg. Az urán először (90-es rendszámú) tórium-234-re bomlik el egy hélium-4 atommag kibocsátásával. Innentől kezdve a folyamat felgyorsul, mert a tórium-234 felezési ideje mindössze 24 nap. És így tovább. Most nem írom le a teljes bomlási láncot, de a végén az ólom-206-os stabil izotóphoz érkezünk majd meg. Habár a kristályba nem igazán tud az ólom belekötődni, ha egy uránatom ólommá válik benne a kristály közepén, azt a kristály nem tudja kivetni magából. Így ha meg akarjuk állapítani, hogy milyen idős az adott cirkonkristály, csak meg kell nézni benne az urán és az ólom arányát. Ebből az urán felezési idejének az ismeretében meg lehet állapítani, hogy mikor szilárdult meg a kristály. Az uránnak vannak más izotópjai is, mint például a urán-235-ös, amely ólom-207-es izotóppá alakul. Így kétféleképpen is megerősíthető a kapott kor. Ezen mérés alapján a legrégebbi cirkonkristály, amit a Földön találtak 4,6 milliárd évesnek adódik (plusz, mínusz néhány millió év). És a jelenlegi tudományos megállapodás az, hogy ez a Föld kora.
De menjünk még visszább az időben. Hány éves a világegyetem? A jelenlegi tudásunk szerint 13,8 milliárd éves. Ezt a világegyetem tágulásából, a kozmikus háttérsugárzásból és egyéb ettől független mérésekből következtették ki. A világegyetem keletkezésének körülményeivel a kozmológia foglalkozik, és még rengeteg a nyitott kérdés ezen a téren.
Az alábbi táblázatban néhány időtartam összehasonlításképp.
| Időtartam | Példák |
|---|---|
| yoctomásodperc, 10-24 s, ys. |
0,3 ys: W és Z bozonok átlagos élettartama 0,5 ys: a t-kvark, átlagos élettartama 23 ys: hidrogén-7 izotóp átlagos élettartama |
| zeptomásodperc, 10-21 s, zs. | 7 zs: a hélium-9-es izotópjának a felezési ideje. |
| attomásodperc, 10-18 s, as. | 12 as: a legrövidebb lézerimpulzus, amit sikerült előállítani. |
| femtomásodperc, 10-15 s, fs. | 1 fs: ennyi idő alatt rezeg az ibolyakék fény egyet oda-vissza. |
| pikomásodperc, 10-12 s, ps. | 1 ps: a b-kvark átlagos élettartama. |
| nanomásodperc, 10-9 s, ns. |
1 ns: ennyi idő alatt halad a fény 30 cm-t. 1 ns: 1 órajel időtartama egy 1 GHz-es processzorban. |
| mikromásodperc, 10-6 s, μs. | 1 μs: Régi 186-os processzoron 1 utasítás végrehajtási ideje. |
| millimásodperc, 10-3 s, ms. |
1 ms: egy emberi idegsejt kisülésének az időtartama. 6 ms: ennyi ideig tart a merevlemeznek 1 adott helyre pozicionálni a fejet. 250 ms: egy szempillantás időtartama. |
| másodperc, 100 s, s. | 1 s: A cézium-133 izotóp két hiperfinom energiaátmenete közötti időtartam 9 192 631 770-szerese. |
| kilomásodperc, 103 s, ks. | 3,6 ks: 1 óra. |
| megamásodperc, 106 s, Ms. |
2,6 Ms: kb. 1 hónap. 31,6 Ms: kb 1 év. |
| gigamásodperc, 109 s, Gs. | 2,1 Gs: ennyi egy ma élő ember várható élettartama átlagosan. |
| teramásodperc, 1012 s, Ts. |
6 Ts: ennyi idő telt el Homo Sapiens kialakulása óta. (200 ezer év) 80 Ts: ennyi ideig tart, míg a fény eljut hozzánk a szomszédos Androméda-galaxisból. (kb. 2,5 millió év) 190 Ts: kb. ennyi ideje vált ketté csimpánz és az emberi faj. (kb 6 millió év) |
| petamásodperc, 1015 s, Ps. |
2,1 Ps: ennyi ideje haltak ki a dinoszauruszok (66 millió év) 7,5 Ps: kb. ennyi idő alatt tesz meg 1 kört a Naprendszer a galaxisunk központja körül (230 millió év) 143 Ps: ennyi idős a Föld. 144 Ps: ennyi idős a Naprendszer. 430 Ps: ennyi idős a Világegyetem. |
| examásodperc, 1018 s, Es. | 312 Es: ennyi ideig világít egy egytized naptömegű vörös törpe csillag. (gyakorlatilag örökké) |
| zettamásodperc, 1021 s, Zs. | 3 Zs: ennyi ideig lehetnek csillagok világon. |
| yottamásodperc, 1024 s, Ys. | 1,64 Ys: feltételezett felezési ideje a bizmut-209-es izotópnak. |
| 102000 s | Ennyi idő múlva lesz a világnak vége a jelenlegi tudásunk szerint. |
Távolságok
Távolságot vagy hosszt legegyszerűbben vonalzóval vagy mérőszalaggal lehet mérni. Ezt már az ókorban is tudták. A mindig kezünk ügyében lévő hosszmérésre alkalmas mérték nagyon sokáig a hüvelyk, arasz, láb és lépés volt. Nyilván ezek a mértékegységek nem valami pontosak, mert minden ember méretei mások. Így aztán előbb vagy utóbb standardizálni kellett a hosszmértékeket is.
A 17. században történt ajánlás a méter definíciójára. Méghozzá 1 méter annak az ingának a hossza, amely 1-et lendül 1 másodperc alatt. Később a 19. században a métert a Föld egyenlítői kerületének 40 milliomod részeként határozták meg. Majd elkészítették a méter etalont, amelyet a Franciaországban őriznek. De később kiderült, hogy nem valami pontos az a méterrúd.
Így végül eljutottunk a méter mostani definíciójához, amit 1986-ban mondtak ki. Kimondták ugyanis, hogy a fény sebessége pontosan 299 792 458 m/s. A métert pedig úgy kell belőni, hogy a fény sebessége ennyi legyen. Ez a jelenlegi definíciója a méternek.
Na de hogyan mérünk távolságokat? Nyilván a kicsi emberi léptékkel felfogható távolságokat mérhetjük mérőszalaggal. Viszont a nagyobb távolságokhoz már máshogy kell hozzáállni. Az egyik módszer az ún. háromszögelés. Az alapötlet az, hogyha egy háromszög egyik oldalát és az azon fekvő két szöget ismerjük, akkor meg lehet határozni a 3. pont távolságát. A távolságot a háromszög csúcsszögével szokták jellemezni, ez az adott távolsághoz tartozó ún. parallaxis.
Ismerjük egy háromszög 1 oldalát és a rajta fekvő két szöget, akkor abból a 3. szög és a másik két oldal hossza a szinusztétel segítségével kiszámolható.
Ha pontosan meg tudjuk mérni a 2 szöget, és ismerjük a 2 mérési pont távolságát, akkor meg lehet határozni pontosan az adott tárgy távolságát. Ilyen módszerekkel meg lehet határozni például a Nemzetközi Űrállomás magasságát, csak 2 embernek 2 városból egyszerre kell lefényképeznie azt. Ilyen háromszögezéssel képesek voltunk megmérni a Hold távolságát is.
Azonban a Nap már túl messze van, ahhoz, hogy a Földről közvetlenül háromszögezéssel mérjük meg. Legalább is abban az időben, amikor sikerült egy pontos becslést adni rá, még nem voltunk képesek megmérni. Túl pici a csúcsszög, hogy közvetlenül megmérjük. Ezért más módszerek kellettek. Az egyik ilyen lehetőség a Vénusz tranzit módszer volt. Nagy ritkán a Vénusz elhalad a Nap előtt. A Föld több pontján is pontosan fel szokták jegyezni ennek a ritka eseménynek a kezdetét és a végét. Az esemény időtartamából ki lehet számolni, hogy milyen messze haladt el a Vénusz korongja a napkorong közepétől. Ebből pedig geometriai ügyeskedéssel meghatározható, hogy milyen messze van a Nap:
A Vénusz Nap előtt való elhaladásának a pontos időtartamának az ismeretében pontosan megmérhető, hogy mekkora látszólagos távolságban haladt el a Nap korongjának középpontja előtt ($\alpha_O$, $\beta_O$). A Vénusz távolságának az ismeretében pedig meghatározható a Vénusz parallaxisszöge is ($\gamma_V$). Ezen szögek ismeretében pedig meghatározható a Nap parányi parallaxisa. Amely alapján a Nap távolsága kb. 150 millió km-nek adódik. (A kép nyilván nem méretarányos.)
A bolygók távolságát nem csak háromszögezéssel lehet megmérni. Hanem radarral is. Méteres pontossággal. A radar elve az, hogy rádióimpulzusokat küld a céltárgy felé, és megméri, hogy mennyi idő alatt ér vissza a jel. Tehát ha a radarjelünk 2 ms alatt ér vissza, akkor oda 1 ms alatt ért. És mivel a rádiójel fénysebességgel terjed, 1 ms alatt 300 km-t tesz meg. Tehát az adott tárgy 300 km-re van. A dolognak a szépsége azonban, hogy nem csak egy objektum távolságát, hanem megfelelő jelfeldolgozással az alakját is meg lehet határozni.
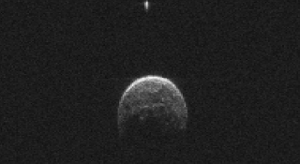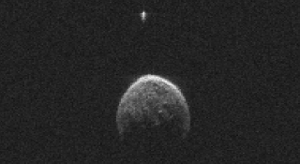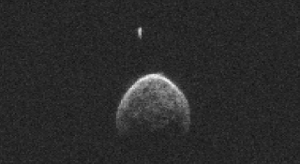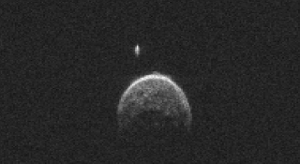
2004 BL86 radarképe. Ez egy kis pár száz méteres aszteroida. Nem csak a távolságát voltunk képesek megmérni, hanem még az alakját is. A képek alapján kiderült, hogy ennek az aszteroidának van egy kis holdja is. (forrás)
A háromszögeléssel a csillagok távolsága is megállapítható. Ez esetben a háromszög alapjának nagyon nagynak kell lennie. A trükk az, hogy a Föld 1 év alatt tesz egy kört a Nap körül. És így félévente pont a Nap átellenes pontján vagyunk. Így kapva egy kb. 300 millió km-es háromszög alapját. Ez már elég nagy ahhoz, hogy a közeli csillagok távolságát meghatározzuk vele. Azonban még ekkor is rendkívül pici csúcsszögekről van szó. A legközelebbi csillag a Proxima Centauri esetén is kb. 0,77 szögmásodpercről van szó (azaz 0,0002 fok). Ez kb. akkora szög, amekkora egy 2 centis bélyeg mérete 6 km-ről nézve, nagyon pici. Ez a legközelebbi csillag is kb. 4 fényévre van, azaz olyan messze, hogy még a fénynek is 4 évig tart, hogy onnan eljusson ide. A 19. századig nem is volt elég pontos műszerünk, hogy megmérjük ezeket a pici szögeket. Aztán ahogy telt az idő egyre jobb méréseket voltunk képesek végezni. Eleinte több száz, majd később több ezer fényévre lévő csillagokat is képesek voltunk háromszögezni. Jelen pillanatban, amikor ezt írom ezen technika csúcsát a Hubble teleszkóp WFC3 kamerája tartja, amely képes 20000 fényév távolságig mérni a csillagokat a parallaxis segítségével.
Habár a mostani technológiával már egész messze lévő csillagokat tudunk háromszögezni, nagyon sokáig csak pár száz fényév volt a maximum távolság, amire alkalmazható volt. Így a még távolabbi csillagok távolságának a kiszámolásához más módszerek kellenek. Ha felmelegítünk egy fémdarabot, akkor egyszer csak elkezd vörösen izzani, aztán egyre fényesebben sárgán, sárgásfehéren, majd végül vakító fényes kékes-fehéren. Ez a szín a hőmérséklettől függ. Ha pontosan megmérjük ezt a színt, akkor ebből ki lehet következtetni az adott tárgy hőmérsékletét is. Tehát így megmérhetjük, hogy milyen a csillag felszíni hőmérséklete. Ezután megmérhetjük, hogy csillagról milyen intenzitással jön a fény. Majd ha a parallaxis alapján ismert a csillag távolsága, akkor meghatározható az abszolút fényesség is. Egy messze lévő nagyobb fényerejű csillag halványabbnak látszódhat, mint egy kisebb fényerejű, de közelebb lévő csillag. A Nap például nagyon fényes, mert közel van. De az égen vannak jóval nagyobb fényerejű csillagok is, amelyek csak a távolságuk miatt látszódnak halványnak. A tudósok összevetették a hőmérsékletet az abszolút fényességgel, és ez alapján kaptak egy érdekes összefüggést: minden melegebb a csillag, annál fényesebb. A következő ábrán látható a hőmérséklet és fényesség közötti összefüggés:
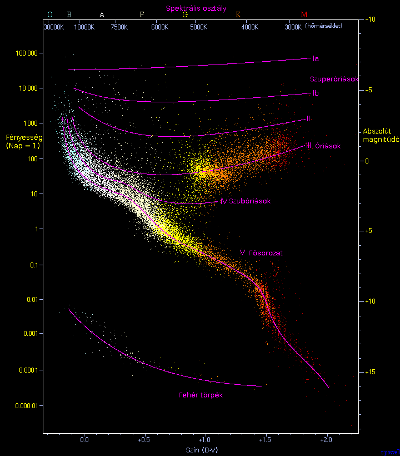
Hertzsprung–Russell diagram. A Hipparcos katalógus csillagai szín és fényesség szerint. A csillagok színe és fényessége között szabályosság figyelhető meg. A csillagok jelentős része ún. fősorozati csillag. Kisebb része óriás vagy törpe. A forró, de halvány csillagok a fehér törpék. A vörös, de nagyon fényes csillagok a vörös óriások. (a képre kattintva meg lehet nézni nagyban. forrás, szerző: Richard Powell, CC-BY-SA, magyarosítottam )
Ebben látszódik, hogy a csillagok nagy része az ún. fősorozati csillag, és annak a színe és a fényereje között egyértelmű összefüggés van. De az is látszik, hogy vannak azért leágazások erről a grafikonról. Például ott lent vannak a törpék, a kiégett csillagok magjai. Illetve ott fent vannak vörös óriások is, amelyek vörösek, de mégis nagyon fényesek, mert az életük végén járnak, és a hidrogén mellett már a héliumot is elkezdték nehezebb elemekké alakítani. A fehér törpék sokkal halványabbak, mint az azonos hőmérsékletű fősorozatbeli csillagok. Olyannyira, hogy akár parallaxissal is mérhetőek. Vörös óriásoknál fordított a helyzet. Ha vörös és túl messze van, hogy háromszögeljük, akkor azt vörös óriásként lehet kezelni, különben vörös törpe. Így amint megállapítottuk a típusát a csillagnak pusztán a földön észlelhető fényessége és színe alapján meg lehet állapítani, hogy milyen messze van az adott csillag.
Ezt az eljárást leginkább a gömbhalmazok és nyílt halmazok esetén lehet tesztelni és kalibrálni. Ezekben ugyanis nagyon sok csillag van egymáshoz közel, és tőlünk nagyjából azonos távolságra.

47 Tucanae gömbhalmaz, amelyben sokféle korú és fényerejű csillag van. A gömbhalmazok alkalmasak a H-R diagram kalibrálására, mert a benne található csillagok azonos távolságra vannak. És fordítva is igaz: a mért fényességértékek és a H-R diagram alapján meghatározható a gömbhalmaz távolsága. (forrás, szerző: ESA/Hubble, CC-BY)
Ha megnézzük a csillagok eloszlását az égen egy sötét, fényszennyezés nélküli helyről (mert ugye ma a sötét hely is ritkaságszámba megy már). Akkor láthatjuk, hogy a csillagok nagy része egy égen körül haladó sávban van. Ennek a magyarázata az, hogy a csillagok nem véletlenszerűen vannak az égen, hanem nagyjából egy síkban. A többi galaxist megnézve miénk is korong alakú.

Ilyen a látvány, hogyha egy fényszennyezés nélküli helyről a galaxisunk közepe felé nézünk. Látható, hogy a csillagok egy egyenes sávban haladnak körbe az égen. ( forrás, szerző: Steve Jurvetson, CC-BY )

Abell 2744 galaxishalmaz. A nagy elmosódott fényes közepű foltok az ún. elliptikus galaxisok, amelyek nem korong alakúak, hanem ellipszoid vagy gömb alakúak. A korong alakú galaxisok jóval kisebbek. (forrás, NASA)
Azt hogy mekkora a galaxisunk, és hogy mi hol vagyunk benne közvetetten lehet meghatározni. A század elején megmérték a gömbhalmazok távolságát és így el tudták helyezni őket térben. Azt találták, hogy ezek a gömbhalmazok eloszlása egy gömb alakot ad ki, amelynek az átmérője kb. 100000 fényév, és melynek a középpontja a Nyilas csillagkép irányában van. Később ettől független mérésekkel is alátámasztották, hogy valóban abban az irányban van a galaxis közepe, és a mi naprendszerünk, kb. 25000 fényévre van tőle.
A távoli galaxisok távolságának a meghatározására megint más módszer kell. A messzi galaxisokban nem tudjuk a csillagokat egyenként megfigyelni, mert az egész összefolyik egyetlen fényes köddé. A módszer ebben az esetben az, hogy várunk, hogy valamelyik csillag felrobbanjon (szupernóva történjen) benne. Egy csillag többféleképpen is felrobbanhat, ami különösen sok információt adhat, az az Ia típusú szupernóva. Az ilyen típusú csillagrobbanás nagyon fényes, és mindig pontosan ugyanannyira fényes. Így a fényességéből nagyon pontosan megállapítható, hogy ez a robbanás milyen messze történt.
De nem csak csillagrobbanásokkal lehet távolságot mérni. Hanem azzal is, hogy megmérjük a távoli galaxisok színét. Minél távolabb van egy galaxis, annál vörösebb a színe. Azaz a fénynek a frekvenciája, amely idejön belőle, jóval hosszabb a hullámhossza, mint a közelebbi galaxisoknak. Ez a kozmikus vöröseltolódás, és hozzávetőlegesen egyenesen arányos a távolsággal. Jelenpillanatban a legtávolabbi galaxis, amiről tudunk a GN-z11. A fény, amit most észlelünk kb. 13,4 milliárd éve indult útnak, és a galaxis most kb. 32 milliárd fényévre lehet tőlünk.
Ezek voltak a nagy távolságok, mi a helyzet kis távolságokkal?
Ha kis távolságokat akarunk mérni, akkor nagyítót vagy mikroszkópot használunk. Azonban hagyományos nagyítóval és mikroszkóppal nem láthatunk a fény hullámhosszánál (azaz 0,6 μm-nél) kisebb részleteket. Ha még kisebb távolságokat szeretnénk látni, akkor rövidebb hullámhosszú fényre vagy részecskére van szükség (mert a részecskéknek, amiket tipikusan golyóknak ábrázolnak, is van hullámhossza). Ilyen rövid hullámhossza van például az elektronoknak, amit az elektronmikroszkópban használnak, azzal már 1 nm nagyságrendű távolságok is láthatók.
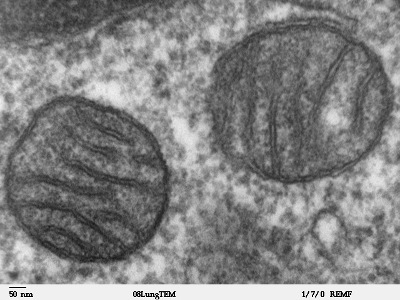
A sejtben található mitokondriumok elektronmikroszkópos képe. Bal alsó sarokban megadott vonal 50nm-nek felel meg. Ezt már fénymikroszkóppal nem láthatnánk. (forrás)
Még kisebb pikométeres távolságok mérésére alkalmasak a kemény röntgen sugarak. Ezek szóródhatnak a kristályok atomjain, majd egymással kölcsönhatásba lépve interferenciaképet hoznak létre. Ennek a segítségével meg lehet határozni a kristályok szerkezetét.

A pöttyök jelentik egy kristályban az atomokat ahogy szabályos távolságokban helyezkednek el. A fekete vonalak jelképezik a bejövő röntgensugarat, a vonalak közötti távolság a röntgensugárzás hullámhossza. A sugárzás az atomokon szóródik és a hullámok interferálnak egymással, mely során erősíthetik, de gyengíthetik is egymást. Abban az irányban erősítik egymást a hullámok, amely irányból nézve az atomok pont a hullámhosszal egyenlő vagy annak egész számú többszörös távolságban látszanak. Valamint annyi erősítés van a fősugár mellett (szimmetrikusan), ahányszor az atomok távolsága nagyobb a hullámhossznál. Esetünkben 3-szor van erősítés a főirányok mellett, tehát a távolság legalább háromszorosa a hullámhossznak. Az erősítések irányából pontosan meghatározható az atomok távolsága, illetve a szabályosan elhelyezkedő atomok sorának a helyzete is.
Egy egyszerű otthon is elvégezhető kísérletet érdemes kipróbálni, ha van egy piros vagy zöld lézermutatónk. A piros lézerfény hullámhossza 671 nm. A rávilágítunk a CD-re, akkor látni fogunk 2 erősítést a visszavert lézerfényben. Ez azt jelenti, hogy a sávok távolsága legalább 1,3 μm, legfeljebb 2 μm. És valóban, a CD-k sávtávolsága szabvány szerint 1,6 μm. Ugyanezt elvégezhetjük DVD-vel is. Ott csak 1 erősítés lesz a két oldalon. Emiatt a sávok szélessége legalább 671 nm, de kevesebb, mint 1,3 μm. És valóban a DVD-k sávtávolsága szabvány szerint 0,74 μm. Ez a játék viszont már nem működik blu-ray DVD esetén. Ott csak a visszavert lézerfényt látjuk, nincs erősítés. Ez azt jelenti, hogy sávok 671 nm-nél is keskenyebbek. És valóban a sávtávolság mindössze 340 nm, kisebb, mint a fény hullámhossza. Ez azt is jelenti, hogy a blu-ray DVD-knek már nincs meg az a szivárványos színjátéka, mint a sima DVD-nek (ezt mondom úgy, hogy még soha sem láttam blu ray DVD-t...).
Minél kisebb távolságokat szeretnénk megmérni, annál kisebb hullámhosszú részecskékre van szükségünk. A kisebb hullámhosszú részecskékhez pedig nagyobb energiára van szükség. A Nagy Hadronütköztetőben 1012 eV energiájú részecskéket ütköztetnek. Ezeknek a hullámhossza elég rövid ahhoz, hogy 10-18 m hosszúságot meg tudjunk mérni vele. Azonban ez nem volt mindig így. Az atommag méretét egész más módszerekkel sikerült meghatároznunk. Fogunk egy vékony fémdarabot és elkezdjük alfa részecskékkel (hélium-4 atommagokkal) bombázni. A radioaktív anyagok bocsátanak ki ilyen részecskéket. Az alfa részecskék nagy része átmegy rajta, mintha ott sem lenne. Azonban egy kisebb része irányt változtat, vagy elveszik. A fémdarab tömegéből meg lehet állapítani, hogy mennyi atom van benne. Illetve, hogy ezeknek az atomoknak mekkora része van kitéve az alfa részecskéknek. Az áthaladó és az irányt változtató alfa részecskék arányából pedig kiszámolható, hogy a fémdarab hány százaléka üres tér, és hány százaléka nem az. Ha feltételezzük, hogy a fémdarab nagyon vékony, akkor jó eséllyel egyik atommag sincs a másik takarásában. Azt találták, hogy szinte az összes alfa részecske átmegy rajta és csak nagyon kevés változtat irányt vagy verődik vissza. Ebből kiderült, hogy az atom jelentős része csak üres tér, és az atommagok által kitakart terület mérete nagyon kicsi, ezt az atomok számával leosztva azt kapták, hogy minden atomhoz egy kb. 10-15 m átmérőjű kör tartozik. És kb. ekkora az atommag.
Ez az atommag méret megállapítható más módon is. Egy korai becslést például úgy adtak rá, hogy arany fóliákat bombáztak alfa-részecskékkel. És azt tapasztalták, hogy kb. 10 MeV energiáig még visszapattannak a részecskék az atommagról, afelett pedig már nem (mert fúzió történik). Milyen közel kell jutnia egy alfa részecskének az atommaghoz, hogy 10 MeV elektromos helyzeti energiát kapjon? Kiszámolták, hogy kb. 10-15 m közel kell kerülnie, amely ugyancsak az atommag mérete.
Az alábbi táblázatban összefoglalok néhány hosszt, és azt, hogy mi az, ami akkora, minden nagyságrend ezerszer nagyobb az előzőnél:
| Hossz nagyságrend | Példák |
|---|---|
| yoctométer, ym, 10-24 m | 20 ym: Kb. ekkora egy 1 MeV-es neutron |
| zeptométer, zm, 10-21 m |
7 zm: nagy energiájú neutrínók mérete 310 zm: a Nagy Hadronütköztetőben lévő 4 TeV energiájú protonok hullámhossza. |
| attométer, am, 10-18 m |
Legfeljebb ekkorák lehetnek a kvarkok. Ebben a nagyságrendben mérhető a LIGO gravitációshullám-detektor érzékenysége. 10 am: Ekkora nagyságrendű a gyenge kölcsönhatás hatósugara. |
| femtométer, am, 10-15 m |
1,5 fm: Ekkora egy 11 MeV energiájú proton. Ekkora nagyságrendű egy atommag. |
| pikométer, pm, 10-12 m |
Ekkora nagyságrendű a gamma sugárzás hullámhossza. 25 pm: hidrogénatom mérete. 31 pm: héliumatom mérete. 154 pm: 2 szénatom távolsága, amely között kémiai kötés áll fenn. |
| nanométer, nm, 10-9 m |
1 nm: szén nanocső átmérője. 2,5 nm: legkisebb tranzisztor egy mikroprocesszorban (2007 óta). 6-10 nm: sejthártya vastagsága. 40 nm: extrém UV hullámhossza. 20-450 nm: vírusok mérete. 380-435 nm: ibolya színű fény hullámhossza. 625-740 nm: vörös fény hullámhossza. |
| mikrométer, μm, 10-6 m |
6-8 μm: vörösvérsejt mérete. 10 μm: Vízcseppek átlagos mérete a ködben. 100 μm: Hajszál átmérője. 750 μm: A legnagyobb baktérium mérete. |
| milliméter, mm, 10-3 m |
5 mm: vöröshangya mérete. 15 mm: egy szúnyog mérete. 42,67 mm: egy golflabda átmérője |
| méter, m, 100 m |
1,7 m: átlagos ember magassága. 33 m: legnagyobb kék bálna mérete (legnagyobb állat). 137 m: gízai piramisok magassága. 828 m: Burdzs Kalifa (jelenlegi legmagasabb épület) magassága. |
| kilométer, km, 103 m |
1 km: 300 kHz-es rádióadás hullámhossza. 8,848 km: A Mt. Everest csúcsának tengerszint feletti magassága. 10,911 km: A legmélyebb árok aljának tengerszint alatti mélysége. 111 km: 1 szélességi fok hossza észak-déli irányban a Földön. 974,6 km: A Ceres törpebolygó átmérője. |
| megaméter, Mm, 106 m |
2390 km: A Plútó átmérője. 3480 km: A Hold átmérője. 6400 km: A Kínai Nagy Fal hossza. 9288 km: A Transzszibériai vasút hossza. 12756 km: A Föld átmérője. 142984 km: A Jupiter átmérője. 299792,458 km: 1 másodperc alatt a fény által megtelt út. 384000 km: A Hold távolsága a Földtől. |
| gigaméter, Gm = 1 000 000 km, 109 m |
1,39 Gm: A Nap átmérője. 18 Gm: 1 fényperc, fény által 1 perc alatt megtett út. 150 Gm: Csillagászati egység (kb. a Föld távolsága a Naptól) 900 Gm: A Betelgeuse csillag átmérője. |
| teraméter, Tm = 1 milliárd km, 1012 m |
1,07 Tm: fényóra, fény által 1 óra alatt megtett út. 1,4 Tm: A Szaturnusz távolsága a Naptól. 2,37 Tm: A jelenleg ismert legnagyobb csillag, az UY Scuti, átmérője. 5,9 Tm: A Plútó távolsága a Naptól. 7,5 Tm: Az Oort felhő távolsága a Naptól (megállapodás szerint) 25,9 Tm: 1 fénynap. Ekkora távolságot tesz meg a fény 1 nap alatt. 200 Tm: Ha az emberi test összes sejtjében lévő DNS molekulát egymás mellé helyeznénk, ilyen hosszú lenne. |
| petaméter, Pm, 1015 m |
7,5 Pm: Az Oort-felhő külső széle (megállapodás szerint). 9,46 Pm: 1 fényév, a fény által 1 év alatt megtett út. 30,9 Pm: 1 parsec. Az a távolság, amelyről az adott tárgy félévenként mért parallaxisa csak 1 szögperc (1/3600 fok). 39,9 Pm: A legközelebbi csillag, a Proxima Centauri. 193 Pm: A legközelebbi ismert exobolygó (más csillag körül keringő bolygó), amely jelenlegi (2010-beni) tudásunk szerint alkalmas életre. 615 Pm (65 fényév): Az első nagy energiájú rádióadásaink kb. ilyen messze jutottak a Földtől (évente adj hozzá 9,5 Pm-et). |
| examéter, Em, 1018 m |
1,9 Em: a legközelebbi csillag, amely pont olyan, mint a Nap (HIP 56948). 9,46 Em: a galaxisunk korongjának a vastagsága. 950 Em: A galaxisunk átmérője (100000 fényév). |
| zettaméter, Zm, 1021 m |
1,54 Zm: a legutóbbi szabad szemmel is látható szupernóva robbanás távolsága (SN 1987 A). 24 Zm: Ilyen messze van az Androméda-galaxis. 60 Zm: A lokális galaxiscsoport átmérője. 300-600 Zm: A Virgo galaxishalmaz távolsága. |
| yottaméter, Ym, 1024 m |
1,9 Ym: A lokális szuper galaxishalmaz átmérője. 13 Ym: A Sloan Nagy Fal nevű galaxis szál hossza. (A galaxis szálak az univerzum legnagyobb léptékű struktúrái, pókhálószerűen járják át a világot és kötik össze a galaxishalmazokat, bennük is galaxisok vannak). 870 Ym: A megfigyelhető világegyetem mérete. 1200 Ym: A világegyetem mérete legalább ekkora. |
És egyelőre ennyi. Tehát ebben a részben megismerkedhettünk két fontos fizikai mennyiséggel: a térrel és idővel. Később még részletesebben belemegyünk majd ebbe.